Project Title : Turbulence as Indicator of Physical Processes at the Heliospheric Interface

Project number: NNH18ZDA001N-HGIO

Science objectives and expected impact of the proposed work

The objectives of this proposal are to perform a detailed analysis of Voyager data and

(1) Create an extensive data base of turbulent properties in the SW and LISM and make it publicly available;

(2) Identify the mechanisms responsible for magnetic field destruction in the IHS and the
recipients of released energy

(3) Investigate the effect of propagating shocks on turbulent
fluctuations in the SW and LISM.

Data analysis techniques

We will perform data analysis in the frequency (and, where possible, wavenumber) space to investigate the nature of turbulent fluctuations in a frequency range
covering almost six decades (1.5 · 10−8 < f < 10−2 Hz). This corresponds to time intervals from 2 years and 48 s. The lower limit is just indicative, since periods will be chosen according to the size of the region to be analyzed. In the IHS at V2, 2-years periods are long enough to catch the largest flow structures. The situation is different at V1, where the flow was rather slow in the IHS and in the LISM. The range of scales analyzed in previous studies will be extended by about three decades. Initially, proper periods for spectral analysis will be identified according to (i) observations from Voyager data on the number of HCS crossings (Richardson et al., 2017) and (ii) HCS kinematic propagation models (Hill et al., 2014; Richardson et al., 2017; Pogorelov et al., 2012b).

Spectral analyses will be performed also for data intervals that start in front of the TS and extend to the HP and further into the LISM (for V1). We will seek for evidence of fluctuations of different nature for sector and unipolar HMF regions.
At scales f & 5 · 10−4 Hz, the MAG instrumental noise affects spectral analysis. However, we plan to resolve even the last decade of the spectrum for (i) characterizing instrumental noise and (ii) detecting phenomena which can still have higher power than that of the noise. Accumulation of magnetic energy at such frequencies may indicate the presence of waves enhanced by the population of PUIs, at frequencies close to their cyclotron scale (see, e.g., Cannon et al., 2014a,b;
Aggarwal et al., 2016). At V2, we will also consider plasma data from PLS. The noise level of these data is higher than that for the MAG data, but we expect to get reliable results at least in the EI range at time scales longer than 1 day. In the LISM, magnetic fluctuations are weaker than in the IHS, and their nature changes as V1 moves away from the HP (Burlaga et al. (2015, 2018)).
Thus, we will identify LISM regions bounded by shocks that can generate vorticity and turbulence, which in turn will interact with pristine interstellar fluctuations.
We will basically use three spectral analysis techniques which complement each other. Spectral analysis gives us information on the distribution of fluctuation energy among scales. Such analysis involves computations of the power spectral density (PSD, or P(f)) of the field components, the spectral anisotropy and spectral compressibility. The parallel (Bk) and perpendicular (B⊥) components of magnetic field fluctuations will also be analyzed. Computing power spectra over a broad
range of frequencies is challenging because of the sparsity of the 48 s data. Gallana et al. (2016) and Fraternale et al. (2016a) have demonstrated that the application of sophisticated techniques makes it possible to recover the spectrum with proper accuracy. The errors have been estimated in terms of spectral slopes. In general, they depend on the frequency range, the method used, the namount and distribution of data gaps, and the signal length. However, we are quite confident that spectra in the IHS can be computed with errors of 10% or lower. The methods to be used for
spectral estimation are the following:

1. Correlation method with linear data interpolation (CI): the PSD is obtained as the Fourier transform of a two-point auto-covariance function computed from linearly-interpolated data. It recovers the spectrum quite well at frequencies smaller than the typical frequency of large data gaps (2 · 10−5 Hz, 12-hr gaps). Due to the low-pass effect of the linear interpolation, a spectral leakage is observed at higher frequencies and the resulting spectral slopes are overestimated.

2. Compressed sensing spectral estimation (CS): a recent paradigm we adopted from the telecommunication data analysis (Donoho, 2006). This method (see examples in Gallana et al., 2016; Fraternale et al., 2016b; Fraternale, 2017) recovers perfectly the high frequency range of the spectrum and gives good estimates in the whole range of frequencies. Depending on the period considered, it may lack accuracy in the neighborhood of the typical large data gap frequency.

3. Optimization method (OP): it aims at minimizing errors in the CI analysis and is especially useful for sparse data sets. This method is based on a genetic algorithm which provides us with a piecewise-linear, model spectrum, which is an approximation of the true spectrum of the Voyager signal (Fraternale, 2017, Chapt).

4). This method helps us reduce the uncertainty in spectral indices and locations of spectral break(s). The technique proved to work well for statistically homogeneous
data sets representing physical phenomena with a continuous spectrum distributed over a broad range of scales. It cannot represent peaks in the spectrum, which are, however, well identified by the other methods above.

Intermittency analysis

Intermittency is a key ingredient of turbulence. Its study gives us information about the non-uniformity of the energy transfer at various scales and provides insight into the dissipation mechanism of fluctuations. There is no doubt that the dissipation range of turbulence has intermittent features. It is clear, however, that due to the resolution intrinsic to the Voyager data, we cannot investigate the dissipative range (except for the high-power wave phenomena, see Fig. 6). We can study intermittency in the inertial range. The structures responsible for dissipation in the SW turbulence may be seen as filaments of vorticity and magnetic flux tubes with the width corresponding to the dissipation scale. The length of those filaments, however, can extend to the largest length scale. Coherent structures may also contribute to the dissipation of turbulent energy. Therefore, some signatures of structures responsible (or related to) magnetic energy conversion can be studied by analyzing the inertial scale. The analysis of intermittency in the inertial range of turbulence spectra is therefore an important part of our project. The intermittent nature of fluctuations
will be investigated by means of both probability density functions (PDFs) of B-increments and by multi-fractal statistics of the locally averaged dissipation (Frisch (1995). As a proxy of the local dissipation, the time derivative (dBi/dt) 2 will be used in place of the tensor
1
2
(∂Bi/∂xi+∂Bj/∂xj )
2
. Limitations are related to the 1D nature of Voyager data, the applicability
of the Taylor hypothesis [(dBi/dt)
2 ∼ V
2
SW(dBi/dr)
2
], and the approximation of derivatives.
Podesta (2017) and Podesta and Roytershteyn (2017) showed the applicability of the proposed approach. 

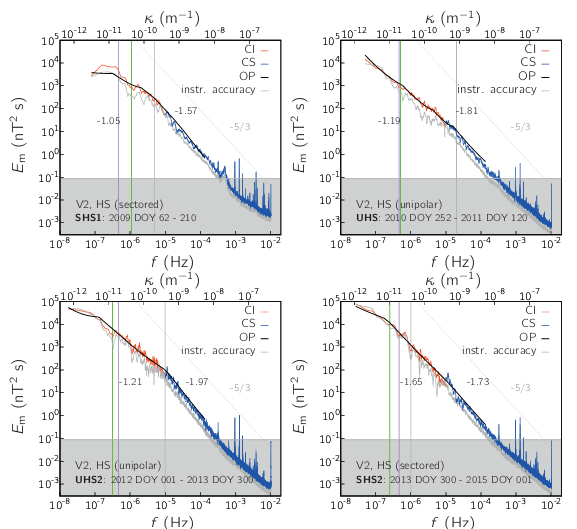
Figure 7: Magnetic energy power spectra in two SHS regions and two
UHS regions. The spectra are computed from three techniques. The
green vertical line indicates fe, the purple line fsun and the grey line the
break frequency f∗. Numbers indicate spectral indices in the EI and in
the IC ranges.