27 Oct Dynamics of Laminar Thin Shear Flows
Dynamics of Laminar Thin Shear Flows
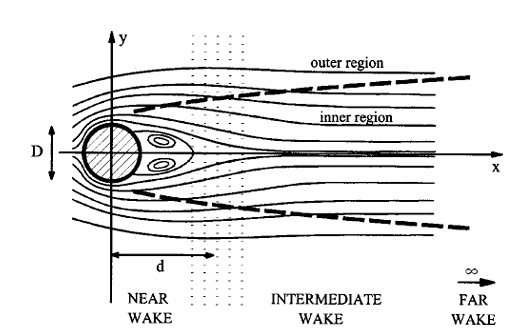
An approximated Navier–Stokes steady solution has been presented for the two dimensional bluff-body wake region that is intermediate between the near wake, which includes the two symmetric counter-rotating eddies, and the ultimate far wake, see Fig. 1.
This approximate solution is here examined in relation to the class of asymptotic solutions that, in the past, were obtained by adopting the rapid decay principle, which implies an irrotational outer flow. The present solution has been obtained by relaxing the imposition of the rapid decay principle. It has been found that, at Reynolds numbers as low as the first critical value and where the non-parallelism of the streamlines is not yet negligible, the division of the field into two basic parts—an inner vortical boundary layer flow and an outer potential flow—is spontaneously shown up to the second order of accuracy: at higher orders in the expansion solution the vorticity is first convected and then diffused in the outer field. If exploited to represent the basic flow of bluff body wakes, the analytical simplicity of this asymptotic expansion is useful for the nonparallel analysis of the instability of two-dimensional wakes. The longitudinal and transversal velocity components are reported in Figures 2 and 3, for different longitudinal stations, x, and different Reynolds numbers.
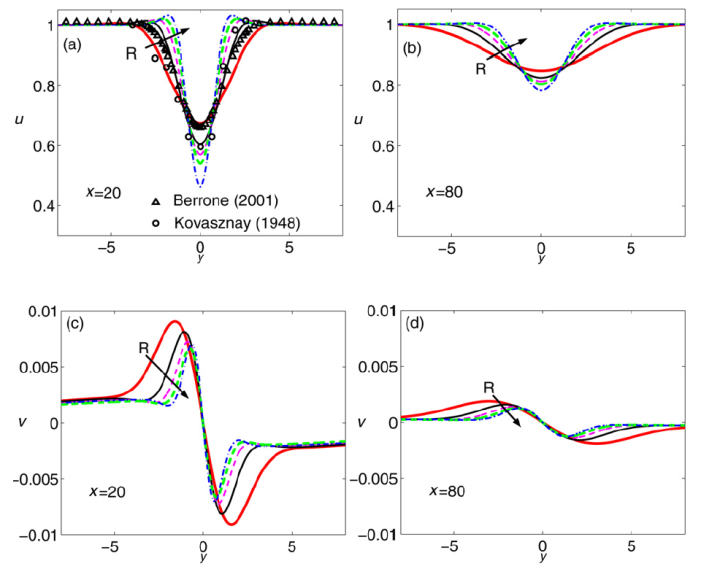
Figure 2.Velocity profiles at the downstream stations x = 20, x = 80 and for R = 20, 40, 60, 80 and 100. (a), (b) Longitudinal velocity u, x = 20 and x = 80, (c), (d) transversal velocity v, x = 20 and x = 80. The comparison with the numerical results by Berrone (2001) (triangles, R = 34, x = 20) and the laboratory data by Kovasznay (1948) (circles, R = 34, x = 20) is shown in part (a).
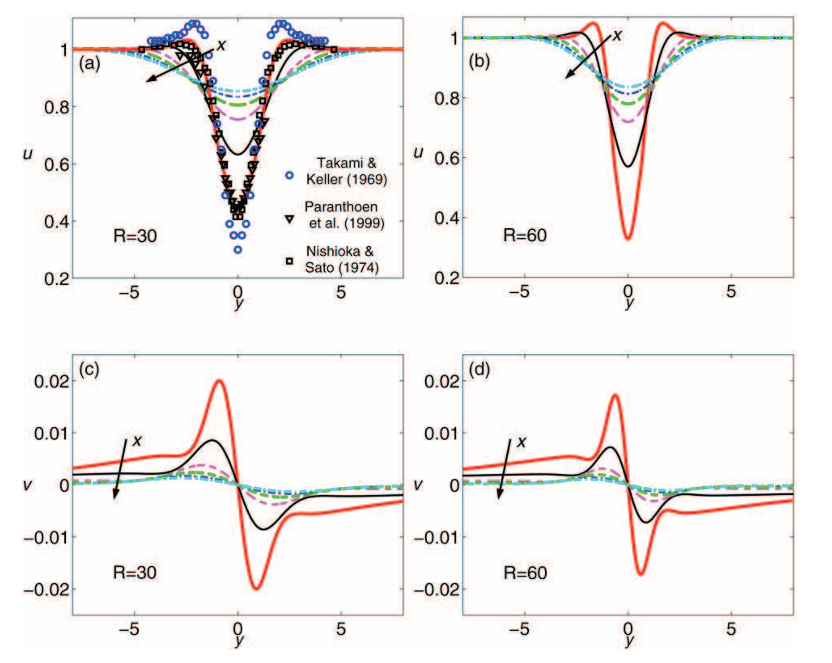

Figure 3. Velocity profiles for R = 30, 60 plotted at stations x = 10, 20, 40, 60, 80 and 100. (a), (b) Longitudinal velocity u, R = 30 and R = 60, (c), (d) transversal velocity v, R = 30 and R = 60. The comparison with the experimental data by Nishioka and Sato (1974) (squares, R = 40, x = 7), Paranthoen et al. (1999) (triangles, R = 34, x = 10) and Takami and Keller (1969) (circles, R = 40, x = 7) is shown in part (a).
An asymptotic representation for the entrainment in the two-dimensional wake has been also analyzed. The representation is obtained from the asymptotic Navier-Stokes solution introduced above. The entrainment, E, is defined as the longitudinal volume flow rate variation in the streamwise direction, dD/dx. The entrainment turns out to be maximum at the beginning of the intermediate region just downstream of the symmetric counter rotating attached eddies, see Fig. 4. Moving downstream, it decreases continuously to zero, which is the asymptotic value in the far field. It increases with the Reynolds number, which is varying in the range between 20 and 100. The spatial evolution of the entrainment depends on the Reynolds number up to a distance of almost 20 body scales. Afterwards, the Reynolds dependence becomes weak. In the Re range here considered, the entrainment can be considered negligible at a normalized distance from the body in between 50–60, that is, a distance value of the same order of magnitude of R.
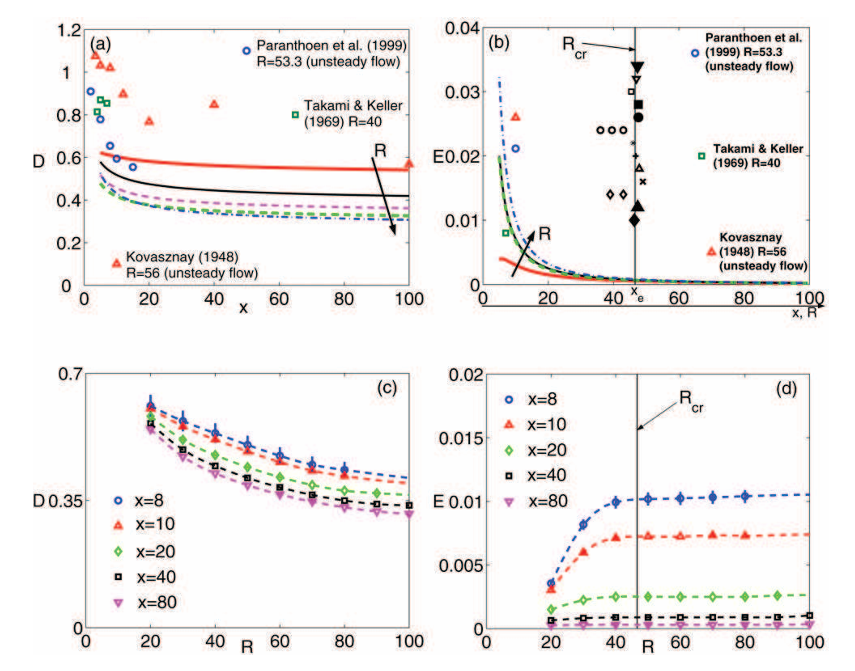
Figure 4. Downstream distribution of the volumetric flow rate defect D and entrainment E for R = 20, 40, 60, 80 and 100. (c), (d): Volumetric flow rate defect D and entrainment E as a function of the R for different stations (x = 8, 10, 20, 40, 80). The values of the volumetric flow rate defect D for the oscillating (supercritical) wake, as inferred from experimental data by Kovasznay (1948, R = 56), Takami and Keller (1969, R = 40) and Paranthoen et al. (1999, R = 53.3), are also shown in part (a). The values of the critical Reynolds number obtained from different numerical and experimental results are placed at a distance from the body, xe, equal to Rcr, see part (b). Position xe is observed to be the wake length where the entrainment is almost extinguished ∀R ∈ [20, 100], which leads to the hypothesis that the steady wake becomes unstable at a Reynolds number that is equal to the normalized distance where the entrainment almost ends and to the value beyond which the entrainment, at a constant distance from the body, stops growing (see part (d)). The symbols represent numerical and experimental data in literature.
Related Publications
- D. Tordella and S. Scarsoglio, The first Rcr as a possible measure of the entrainment length in a 2D steady wake, Physics Letters A, 373, 1159–1164, 2009.
- D. Tordella and M. Belan, A new matched asymptotic expansion for the intermediate and far flow behind a finite body, Physics of Fluids, 15 (7), 1897-1906, 2003.
- M. Belan and D. Tordella, Asymptotic expansions for two dimensional symmetrical Laminar wakes, ZAMM-Zeitschrift für Angewandte Mathematik und Mechanik, 82 (4), 219-234, 2002.



