Hydrodynamic Stability 2
1957
post-template-default,single,single-post,postid-1957,single-format-standard,wp-custom-logo,theme-bridge,bridge-core-3.3,qi-blocks-1.3.4,qodef-gutenberg--no-touch,woocommerce-no-js,qodef-qi--no-touch,qi-addons-for-elementor-1.8.1,qode-quick-view-for-woocommerce-1.1.1,qqvfw--no-touch,qode-wishlist-for-woocommerce-1.2.4,qwfw--no-touch,qode-page-transition-enabled,ajax_fade,page_not_loaded,,qode-title-hidden,columns-4,qode-theme-ver-30.8,qode-theme-bridge,wpb-js-composer js-comp-ver-7.9,vc_responsive,elementor-default,elementor-kit-136,elementor-page elementor-page-1957

04 Nov Hydrodynamic Stability 2

Posted at 12:27h in Software by
0 Likes

Hydrodynamic Stability 2

Nonmodal linear stability via the Galerkin method using Chandrasekhar functions expansion

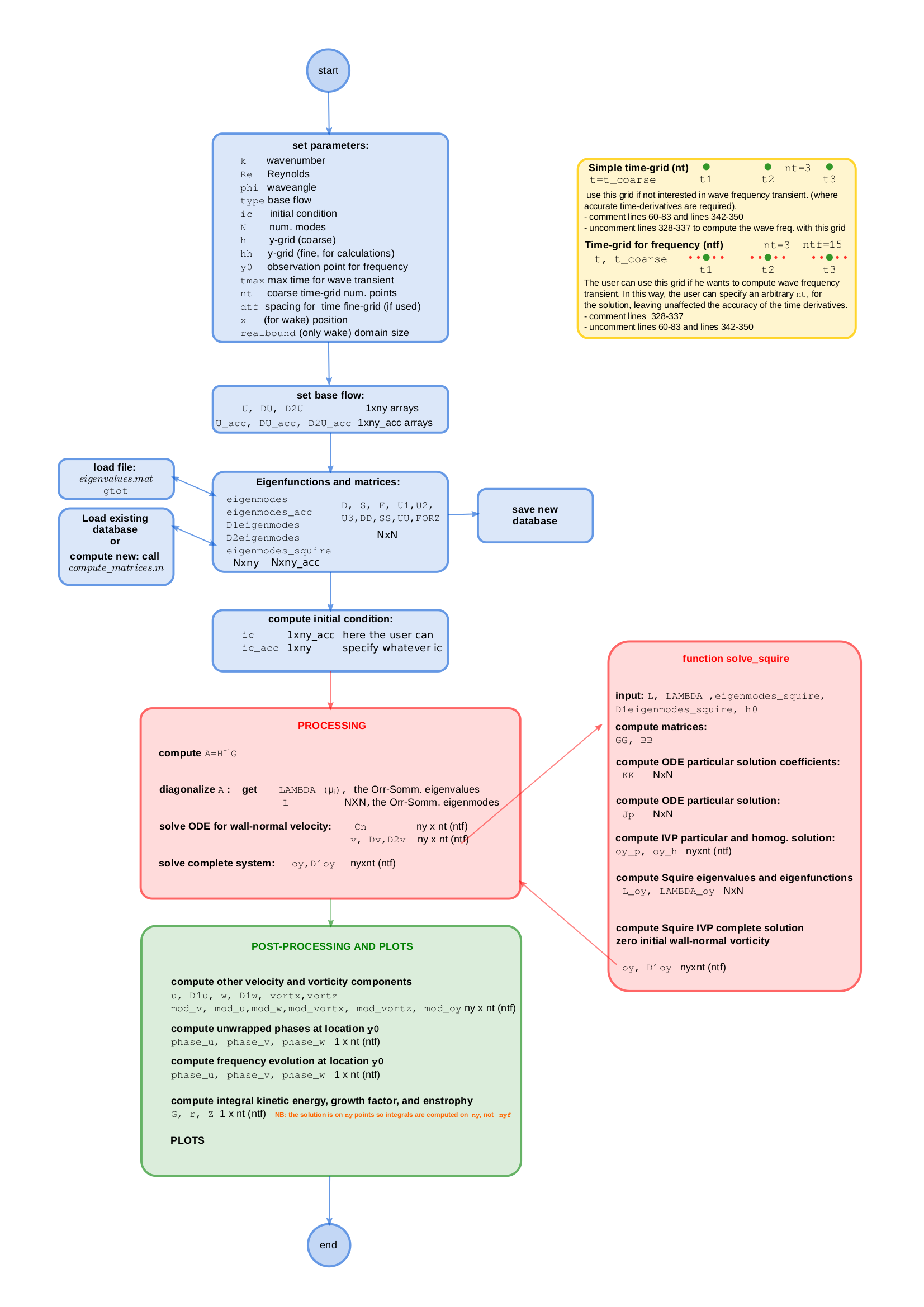
These codes solve the Orr-Sommerfeld/ Squire Initial Value Problem for linear,  three-dimensional, wave perturbations in shear flows. The solution is computed by a semi-analytical procedure. Starting from the velocity-vorticity formulation, the solution is expressed in terms of normal eigenfunctions expansion and the problem is reduced to a set of ODEs via the Galerkin variational procedure. We use the Chandrasekhar eigenfunctions for the velocity, and Fourier for the vorticity, providing a 5th order of accuracy. The method is implemented in Matlab, and the code consists of four scripts.

Find below the complete documentation for the method and the code.  Just some information:

  • The code solves the Orr-sommerfeld/Squire nonmodal and modal problem;
  • Only no-slip boundary conditions are considered;
  • The computation is fast (order of 1 minute per simulation);
  • The user can specify any parallel base flow (bounded, arbitrary domain size), and any initial condition for the velocity;
  • The user can define arbitrary time and spatial grids (please see the documentation for all the details);                                                                          Code Development and Versions

All the codes have been developed and maintained by our group:

      • Version 0 (2013): the first version was published in the Master’s theses of Federico Fraternale.
      • Version 1.0 (2014):  arbitrary y-domain included to study the frozen-wake flow with homogeneous boundary conditions for the perturbation; other numerical improvements.

Software Download

          • Documentation  [PDF] 
          • Stability code v1.0 for plane Poiseuille, Couette, and Wake flows [DOWNLOAD]